Tutorial: Functional Requirements of Software Systems

Functional and Nonfunctional Requirements

Requirements of software systems can be Functional or Non-functional.

Functional requirements define the required behavior of the system to be built, as reported by a hypothetical observer envisioning the inputs that the future system will accept and the outputs it will produce in response to those inputs.

Non-functional requirements specify additional properties of the system to be built, other than functionality. Non-functional requirements can be subcategorized into categories such as external interface requirements, performance requirements, design constraints, logical database requirements, and “characteristics” (termed “attributes” in IEEE Std. 830) that don’t fit neatly into any of the other categories.

In this tutorial we will focus on functional requirements exclusively.

What Functional Requirements Are Not

The functional requirements sections of specifications often tend to be “laundry lists” of statements in the form, “the system shall…” relating to “capabilities” of the system, not functions. For example, “the system shall have the capability to update an inventory database.” Or, “the system shall have the capability to retrieve inventory information and present it to the user.”

The problem with these “requirements” is that they are not functional requirements at all, because, in both cases, the inputs are missing from the statement! One might say, “Well, obviously, the system will update the inventory when it receives an update transaction from the users.” Yes, but it isn’t stated. Similarly, one must infer that a user request will trigger the retrieval of inventory information. But different readers may make different inferences, particularly when requirements are complex, and may reach vastly different conclusions about what is required. These statements are ambiguous, because they can mean different things to different people.

The statements are also incomplete: they do not specify which data elements will be updated, or retrieved, or presented to the user. They also do not say what the system is required to do if, say, the information to be updated or retrieved is missing from the database.

Because the inputs are missing, the statements are inherently un-testable as well. So, when the system test team, or the acceptance test team, starts to develop test scenarios, the team members will likewise make assumptions that may vary with the users’ intent.

Functional Requirements: A Simple Definition

If functional requirements are not capabilities of the system, what are they? Formal definitions of requirements almost universally agree on this essential characteristic of a functional requirement: it defines a transformation of inputs into outputs. The classic definition of a function, which we learned in seventh or eighth grade, is:

y = f(x) (1)

In English, “y is a function of x.” If the function belongs to an information system, x is the input to the system, and y is the output, or the response to that input.

Example: suppose we have a mortgage calculator program. It accepts three input parameters: the annual interest rate, the principal amount to be borrowed, and the number of monthly payments. The output is the amount of the monthly payment. If we enter 6.0% as the interest rate, $100,000 as the principal amount, and 360 as the number of payments (e.g., one payment a month for 30 years), the program calculates the monthly payment as $599.55. If we come back five minutes from now, or two weeks from now, or 20 years from now, and ask exactly the same question, we’ll get exactly the same answer: $599.55. This illustrates y=f(x), where the output is a function of the current input – and not a function of anything else.

Functional Requirements: A More Formal Definition

But there’s a problem with this simple equation. Most of the information processing applications we are familiar with do not necessarily produce exactly the same response to a given input each time, because the system retrieves some of the response from its memory, and the content of its memory tends to change over time.

For example, if we enter a request for the content of the record for Customer 12345, John Doe, who lives at 123 Main Street, Anytown, MA 01899. We should get:

Table 1. Initial Values of Record for Customer No. 12345

Let’s suppose that, some time later, we make exactly the same request: we want the content of the record for Customer 12345: This time we get:

Table.2. Updated Values of Record for Customer No. 12345

The second response yielded different results from the first response, because John Doe has apparently moved from 123 Main Street to 456 Side Street. So our simple equation doesn’t work. If it worked correctly, we’d get exactly the same response every time we made that specific query. To fix the problem, let’s modify the equation as follows:

{y}, {FS} = f({x}, {IS}) (2)

where {y} is a set of externally visible responses, i.e., responses that are visible outside the system; {x} is a set of inputs; {IS} is the initial state, i.e., the initial values of a set of state variables stored inside the system when the request is made (when {x} is entered), and {FS} is the final state, i.e., the set of values of the same state variables stored inside the system when the system finishes executing the function.

In English, {y} and {FS} are a function of {x} and {IS}.

In this example, the final state would be equal to the initial state, because we retrieved information without changing it. If we did an add or an update, or a delete transaction, then the final state would differ from the initial state.

The notion of sets instead of individual inputs arises from the observation that information systems typically accept more than one input at a time in a given transaction (and may produce more than one output at a time in a given transaction). For example, in our simple mortgage calculator, the program accepts a set of three input parameters at once, and bases its calculation on the values of all three.

By the same token, a given set of inputs is quite likely to produce more than one response. For example, in a log-in function, the user enters an ID and password. In response, the system does all of the following: authenticates the ID/password combination; records the user ID, date, time, and location (workstation ID, for example) of the log-in transaction; activates a token enabling the user to perform additional functions for which the given user has privileges; and notifies the user of a successful log-in. That’s why we talk about a set of responses, not just a single response.

The state information may be more difficult to grasp. “State” represents, in essence, the instantaneous set of values of the memory of an information system. When we change a single character (or even a single bit) of the memory, we are changing the state of the machine. The state encompasses the main memory and all of the secondary memory (e.g., hard drives) connected to the computer. Conceptually, the memory consists of one enormously long string of bits. If, for example, our computer has 100 Gbytes (800 Gbits) of disk space, then its number of distinct states is roughly [(2) raised to the (800 billion)] power. That’s approximately 240 billion different distinct states.

Fortunately, we usually aren’t interested in the state of the entire machine, because we only use a piece of it at a time. For example, going back to our earlier Customer 12345 example, we really only care about the part of the memory devoted to the record for that particular customer. Indeed, one possible value for the fields of that record is <not found>, if the record isn’t in the customer table. But if the record is there, as in the example above, its state is represented by the values in its fields. If we create the record, we are creating values for all the fields, comprising the final state of the add transaction. If we subsequently update any of the fields, as in the earlier example, we are changing the state accordingly. If we decide to delete the record (or if we never enter the record in the first place), then the state of all of the fields is <not found>, and we expect to get an error message when we look for the record.

Summary

The point of this discussion is that a full definition of a function for an information system takes into account state information as well as external inputs. Also, part of the response of the system, {FS}, may include changes to the state information. So, a given function has an initial state, {IS}, which is the state of the relevant information when the inputs arrive, and a final state, which is the state of the relevant information when the program has finished processing the inputs – perhaps only a few nanoseconds after the inputs arrive. For example, the customer’s street address in Table 2 above, 456 Side Street, is different from the street address in Table 1, 123 Main Street. When the update occurred, the state of the record changed.

This discussion, summarized in Figure 1, establishes a conceptual framework for writing functional requirements.

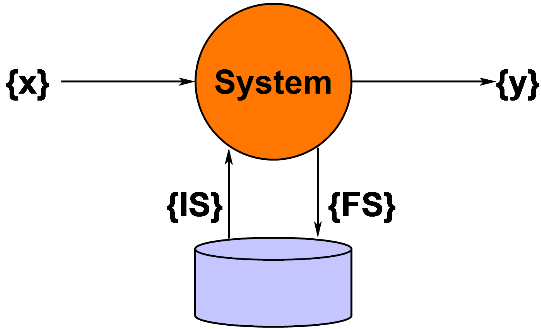
Figure 1.. Components of a function.

Note that we’ve also solved the testability problem. If our stated requirement defines {x}, {IS}, {y}, and {FS}, it fulfills the description of a test case! We can run the test by storing {IS} in the system, applying {x} to invoke the function f, and look at the output to see if the various specified parts of {y} and {FS} are observed as a result of f.

Specifying Complex Functionality

The example given in this tutorial is purposely simple, to explain the concepts. What happens in the real world, when functions are more complex? The model in Figure 1 still applies, although more effort may be required to specify complex algorithms. If the system in question accepts inputs one at a time, the model can be applied directly, no matter how complex each function may be. However, triggering events can overlap in time, e.g.:

• {X1} invokes F1, and F1 begins to execute
• Before {X1} finishes, another input, {X2}, arrives to invoke F2
• The initial state {IS2} must take into account any changes in state that F1 produced that are visible to F2. (Note: If F1 and F2 do not rely on shared state information, {IS2} will be the same whether F1 is running or not when F2 begins.)

This issue of handling functions that execute completely or partly in parallel makes the specification more difficult to write. A discussion of techniques for dealing with this issue is beyond the scope of this elementary article.

How to Learn More about It

Courses

• More information on testing is given in the two-day course Effective Software Testing (SWT, 2 days)
• Requirements management is addressed in the two-day course Software Configuration Management. (SWCM, 2 days)
• The connection between requirements and project estimation is addressed in the two-day course Software Project Estimation (SWPE, 2 days)

Books

• Cockburn, Alistair. Writing Effective Use Cases. Addison-Wesley, 2001.
• Cohn, Mike. User Stories Applied: For Agile Software Development. Addison-Wesley, 2004.
• Robertson, Suzanne, and James Robertson. Mastering the Requirements Process. Addison-Wesley. 1999.
• Weilkiens, Tim. Systems Engineering with SysML/UML. Morgan-Kaufmann/OMG Press, 2007.
• Wiegers, Karl. Software Requirements, Second Edition. Microsoft Press, 2003.

Web Resources

• Use case fundamentals. http://alistair.cockburn.us/index.php/Use_case_fundamentals.